Hopefully, gentle introduction to neural networks

From apps that let you see how you may look like when you are old, to human-masters-beating AI of Alpha GO, to self-driving cars, neural networks are playing bigger and bigger role in our lives potentially leading to artificial intelligence being no longer "artificial", but what are they?

Before I start, please be advised that this post is written in such a way that people without mathematical background can grasp the idea of neural networks. That's why there will be a lot of simplifications and non-professional nomenclature usage. I do not have a deep learning PhD, and my experience comes from working on my own neural network library.

What is neural network

One way to think about neural network is a black-box that accepts bunch of numbers (input) and spits out some other numbers (output).

That on it's own wouldn't be too useful, right? That's why we can train that black box to spit out the number we expect based on what we throw into it. What is great about it, is that after training is complete, it will produce outputs for inputs it has never seen before. In that case, it will try to approximate an output based on what we have shown it while training.

What is inside the blackbox

Now that we know, how network works on a higher level, let's take a look under the hood. If take the "cover" off, we will notice there is more interconnected blackboxes.

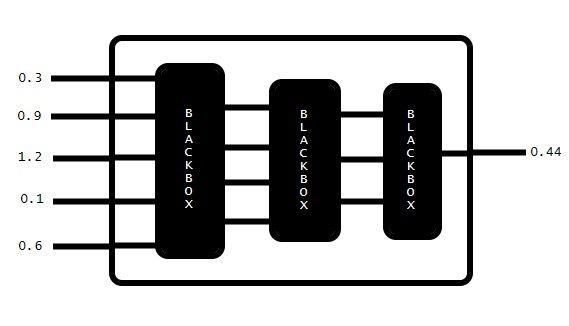
These are called layers. The beauty and complexity of neural networks comes from the fact that entire network (the original blackbox) can be used inside another network. It's like inception...

Quick note on the "deep" learning

Word deep is commonly used in conjunction with neural networks and learning. It comes from the fact that any network with more than 2(or 3) layers in-between first layer and the last layer is referred to as deep neural network. These days, pretty much every non-trivial network is deep because it easily has several dozen layers. Process of training deep network is called nothing else but deep learning.

A sneak peek into a 'simple' layer

We have a dozen or so layer types commonly used in neural networks, but their job is always the same: apply some kind operation to an input in order to generate output. Here is how a densely connected layer looks inside.

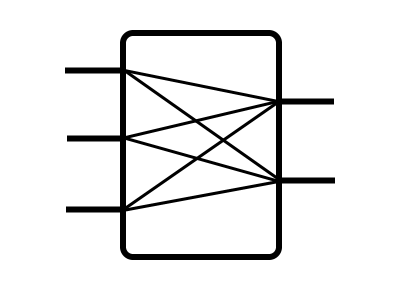
Most of the time an operation uses some parameters (usually called weights), which can be modified during training. Same applies to entire network, because it can be used as a layer. In that case we are dealing with even more complex operation being combination of operations of all internal layers and even more weights.

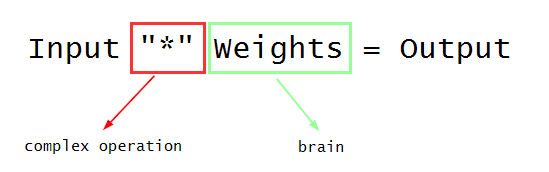
Weights in the picture above are considered a brain of a layer/network, because they determine an output.

How to train a network

Process of training a network is called back propagation and may look very complex when looking at the math behind it, but the overall idea is pretty straight forward.

For simplicity, let's say we want our network to figure out that result of multiplication of 3 by 2 is 6.

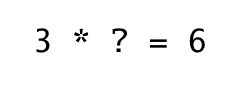
If we input 3 to the network without any training we will get some random output number, because at this point our weight is completely random. While training a network is given input and output, and it has to learn the weights (its brain). So how could we do that?

Even thou in our simple example we could just divide 6 by 3, we have to remember that in case of neural networks "*" is a very complex operation, which is not easily reversible. Fortunately, there is a way to learn the weight without reversing the operation. In order to do that we need to know how far are we from the correct output.

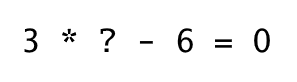
We can calculate that by subtracting it from the predicted output. If result is zero, it means the weight is correct and out network has learned successfully. This most likely will not be the case at the beginning of a training process, so the weight will have to be modified somehow.

Training step

If instead of zero we get a positive value it means the weight is too big and we should decrease it a little bit, if negative, it should be increased instead, to get us closer to zero. This kind of resembles playing the guessing game.

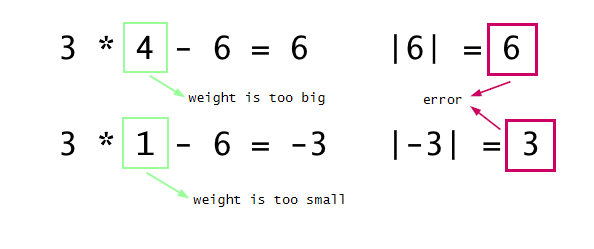
The closer the error is to zero the smaller steps we should take, otherwise we may keep overshooting the correct value. This is why the amount of weight change should be the error multiplied by a small number (since we are taking little steps). In our example we are changing the weight by a fraction of error in the direction based on the sign of the guess result. That fraction is usually anything between 0.1 and 0.0001 and is called the learning rate. The smaller it is the closer we can get to the correct solution, but we will have to take more steps to get there. It it is too big there is a risk of endless oscillation around the correct weight value.

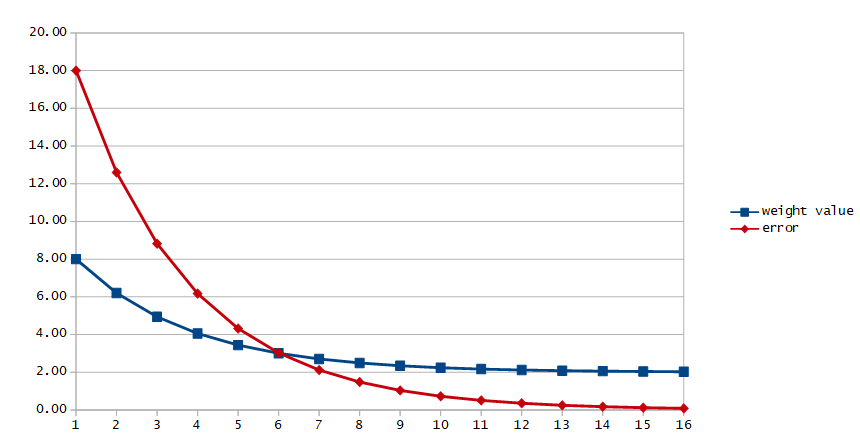
Above you can see how weight would changes each step when using learning rate 0.1. It started from 8 and around step 13 it reached almost exactly 2. Normally the training is stopped when error is small enough, meaning our network learned its weights.

In this simple example we had only one weight, one input value, one output value, one sample, and we instinctively knew which way to go depending on the result. In the real-life networks we commonly have millions of weights, thousands of inputs and outputs, huge samples data-sets and we use derivatives to figure out which way and by how much to modify each weight.

Conclusion

So far, I hopefully provided a high-level overview of what neural networks are, how they work and how to train them. In the next post, I will write about neural networks applications and how they can be used to generate art.